中国石油大学 | 基于最小维修的石化安全设备区间截尾寿命数据分析

主要内容：在石化安全关键设备寿命截尾数据的可靠性评估过程中，为避免传统可靠性评估方法未考虑维修对故障间隔时间的影响，以及中值填充法误差较大的缺点，本文提出了一种逆变换区间截尾数据填充方法。首先，在可修系统基于最小维修的假设下，通过非齐次泊松过程描述系统的故障趋势，利用逆变换填充得到监测区间的缺失数据；随后根据蒙特卡罗期望最大化算法，获得填充数据的参数估计值。通过蜡油加氢装置紧急泄压阀的案例分析，该算法能够很好地融合已有数据，得到的形状参数估计值偏差与中值填充法相比缩小4%以上，从而验证了该算法的有效性；这有助于安全关键设备的定量化完整性管理，保障石化装置平稳运行。

关键词：石化设备；安全；数值分析；蒙特卡罗模拟；参数估计

在石化企业中，安全关键设备的可靠性很大程度上决定着企业的安全生产水平，一旦此类设备发生故障，装置的动态风险水平就会受到影响。因此，对设备进行可靠性分析、实时掌握设备可靠性状况具有十分重要的意义[1-2]。在工业现场复杂安全关键设备（一般为可修系统）投入正式使用后，会暴露许多与设计方案、运行环境、操作方法和维护策略等相关的故障和缺陷。对于可修系统而言，当系统出现故障时，对系统进行维修，使其恢复正常运行，因此可修系统的寿命周期通常经历运行→故障→维修→运行的循环过程。

当前研究可修系统可靠性的方法主要有马尔可夫过程和随机点过程[3]，其中马尔可夫过程主要针对可修系统存在的多状态问题，通过描述多种状态之间的转移概率来获得系统的可靠性水平。随机点过程则重点关注系统的故障间隔运行时间，研究系统的运行和故障两种状态，而不同的随机点过程代表着不同的维修类型，其中更新过程、齐次泊松过程代表“修复如新”的维修类型，非齐次泊松过程代表“修复如旧”，而广义更新过程代表“不完全维修”的维修类型。此外，由于受监测周期、经费等外部条件的限制，导致故障时间记录缺失或无法判断具体的故障时间，即所谓的区间截尾数据问题[4]。针对区间截尾数据的情况，国内外学者提出了一些数据处理方法，Xiao 等[5]尝试用分位数填充算法将区间截尾数据转化为经典统计学方法可以使用的虚拟完全数据，同时对该算法进行了性能分析；彭新凯等[6]提出一种针对区间截尾数据的分位数填充算法，用于石化设备的可靠性评估，然而他们并未考虑维修活动对故障间隔时间的影响；考虑到故障数据的不完整性，Sharareh 等[7]提出使用似然比方法检验故障数据的趋势，通过期望最大化（EM）算法获取参数的估计值，但存在着复杂的期望计算。

针对传统的可靠性评估算法假设设备寿命时间独立同分布的缺陷，以及工程上常用的中值填充法（MPA）又存在分布参数估计不准确的缺点。在可修系统基于最小维修的假设下，提出一种逆变换区间截尾数据填充算法，随机地填充出缺失的故障时间，解决了区间缺失数据难以处理的问题，便于工程中实际应用，最后以蜡油加氢装置系统中的紧急泄压阀为案例，将该方法得到的参数估计值与传统中值填充法进行对比，以说明逆变换填充算法的优势与数值性能。

1 可修安全关键设备的数学模型

1.1 可修系统的最小维修模型

随机点过程的前提是假设一个可修产品在t=0时刻投入使用，当系统出现故障时进行维修，使其恢复正常运行；在该系统第二次出现故障时，仍然进行维修工作，以此类推，在忽略维修时间的前提下，则可以得到故障时间序列。设N(t)为在(0,t]内的故障个数，则N(t)构成一随机过程，称这个特殊的随机过程{N(t), t≥0}是一个随机点过程。在随机点过程中，非齐次泊松过程则代表了“最小维修”的过程，该维修活动将一个故障的系统修复到可以工作的状态，其中幂律过程（PLP）是非齐次泊松过程（NHPP）的最基本模型，其故障强度函数可用式(1)表示。

当0＜η＜1时，故障时间间隔随机增加，系统处于可靠性增长过程中；反之，当η＞1时，故障时间间隔随机减小，系统处于可靠性下降过程中；当η=1时，非齐次泊松过程退化为泊松过程，故障率为常数，故障时间服从指数分布。

Oscar 和Folks[8]称满足式(1)和式(2)所示的威布尔过程，分别为可修产品的故障强度函数和累积故障次数的均值函数。尽管故障强度函数的表达式与不可修产品双参数威布尔分布的故障率表达式相同，但本质上两者有很大的区别。在可修系统中，产品的平均首次故障时间是描述其首次故障状况的一个可靠性指标，相当于不可修产品的寿命问题，此时可修或不可修产品的故障时间一般都服从威布尔分布。然而考虑到设备维修活动对设备故障率的影响[9]，可修产品第二、三…次故障的间隔时间并不服从以(β,η)为参数的威布尔分布。

1.2 寿命数据的统计推断

2 逆变换区间截尾数据填充算法的参数估计

针对可修系统的区间数据截尾（censored）情况，由于无法确定具体的设备故障时间，因此将故障时间归在前后两次周期性监测的时间区间内，如图1 所示。在某一监测机制下记录系统的故障情况，T 为 一 个 监 测 周 期，令0＜t′1＜t′2＜…＜t′k - 1＜t′k≤T 表示一个监测周期内每个观测区间的右端点值，k为该监测机制下的区间数；n1,n2,…,nk表示每个观测区间内的故障个数。

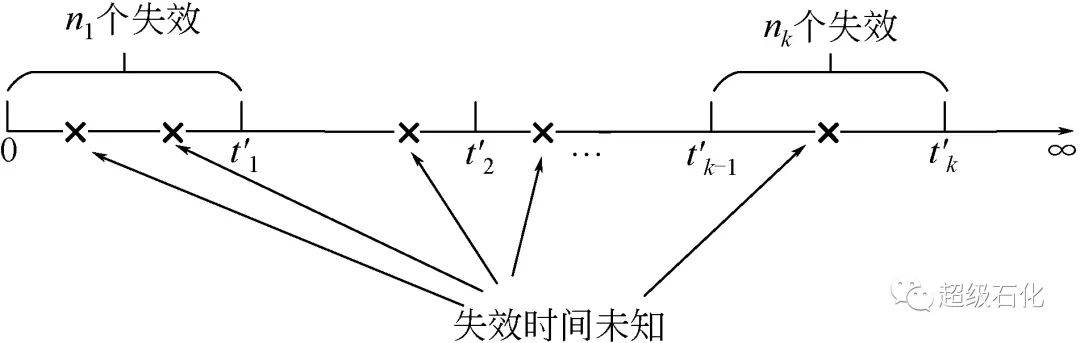
图1 区间截尾数据

令1≤i≤k，当观测区间的故障个数ni给定时，则{t′i(1),t′i,(j),…,t′i,(ni)}表示区间(t′i- 1,t′i]故障时间的次序统计量；根据NHPP的特性可得缺失数据的条件概率密度函数［式(11)］。

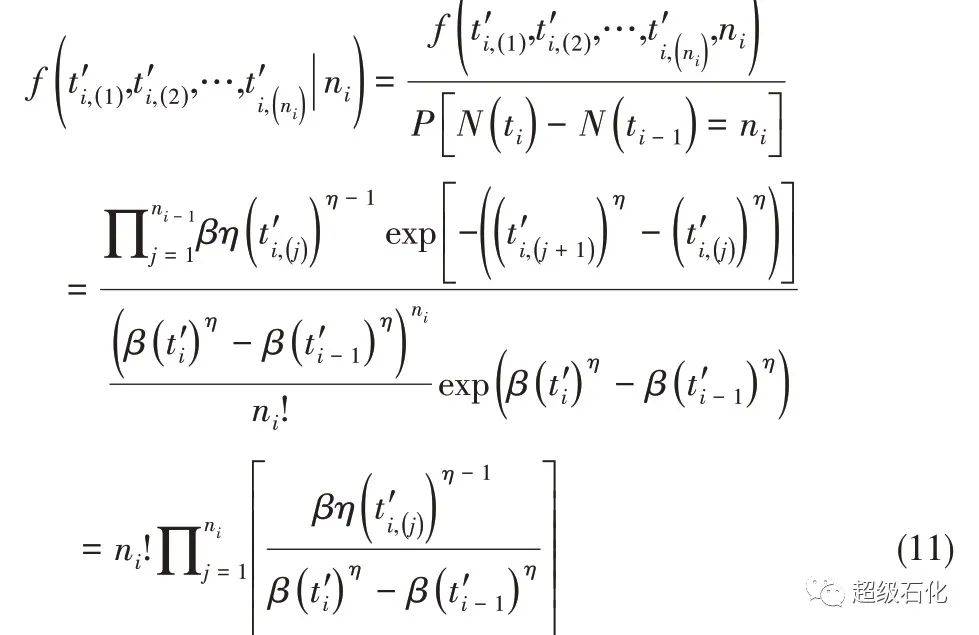
其中1≤j≤ni，由于故障时间的次序统计量，其联合概率密度函数含有多个相互影响的时间次序变量，所以不能直接对其进行区间缺失数据的填充。

为此本文提出逆变换区间截尾数据填充算法（逆变换区间截尾数据填充算法，ITFA），其流程如图2 所示。首先根据式(11)得到可修系统在区间(t′i-1,t′i]中发生ni次故障的随机变量t′i,j的概率密度函数[11]［式(12)］。

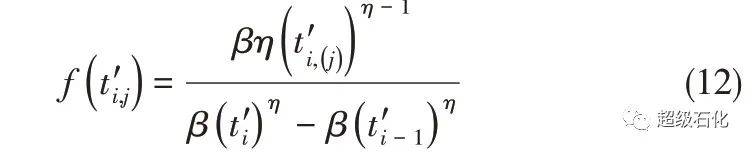
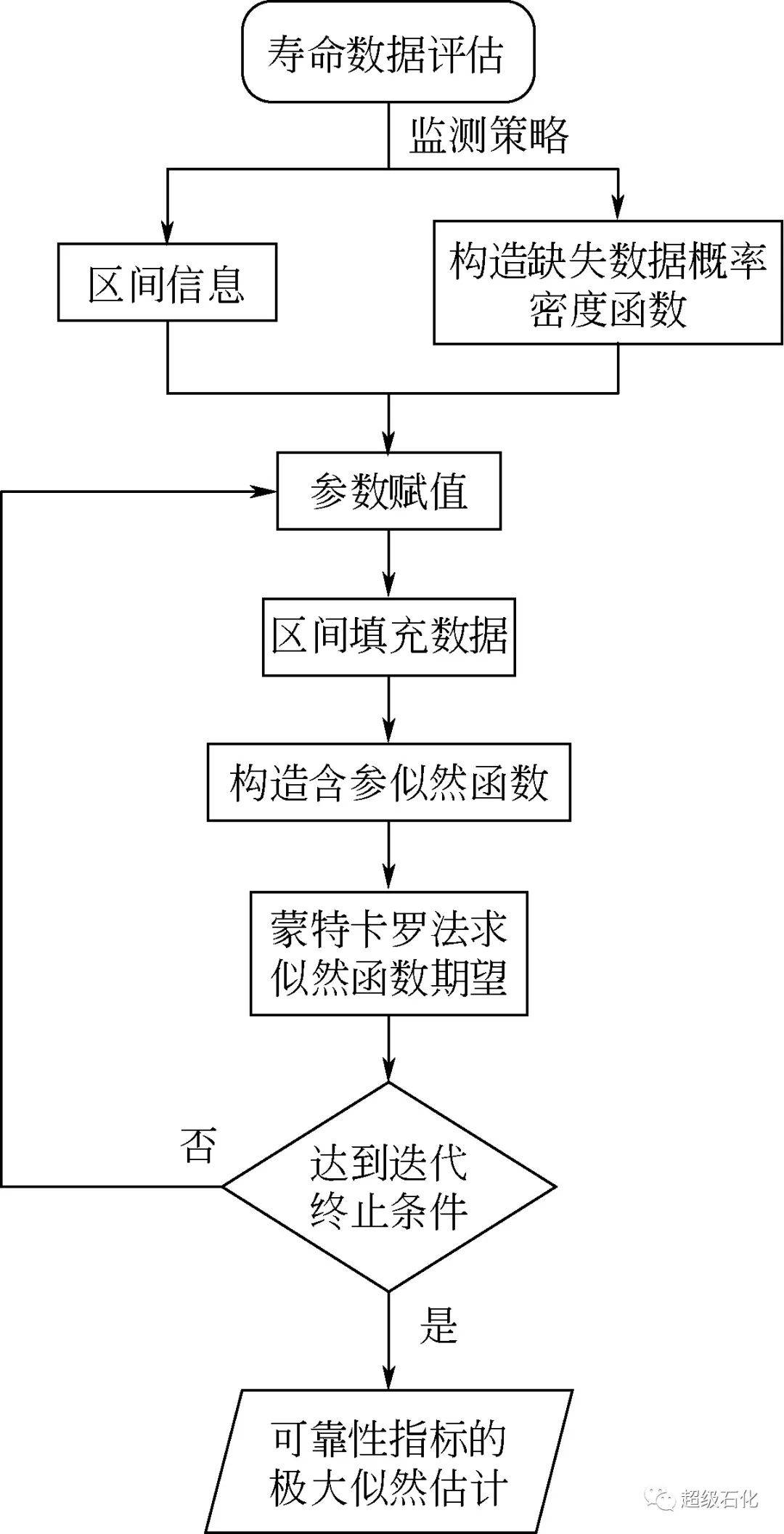
图2 逆变换区间截尾数据填充算法ITFA的参数估计流程

其中t′i-1≤t′i,j≤t′i，所以可根据该概率密度函数对缺失数据进行填充。假设随机变量X服从(0,1)上的均匀分布，生成xj个随机数j=1,2,…,ni，利用逆变换区间截尾数据填充算法随机地填充出区间(t′i-1,t′i]缺失的故障时间［式(13)］。

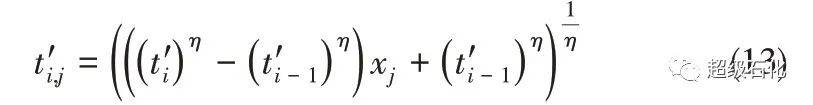
该算法将多维且相关的缺失数据集转化为多个一维且独立的数据，简化了区间缺失数据的填充过程，实现了缺失数据的高效插补。值得注意的是，由于故障强度函数中的参数未知，因此利用蒙特卡罗最大期望算法（MCEM）处理数据缺失情况下的参数估计问题[12]，以该样本均值对样本总体均值进行描述，避免了复杂的期望计算。

令Z表示参数评估所需的故障数据集，其中Z0表示每个观测区间的故障个数{n1,n2,…,nk}，Y 表示具体的区间缺失数据{t1,t2,…,tr}，r=n1+n2+…+nk表示整个监测周期的故障个数。

E步：

在寿命数据的全样本观测下，根据式(4)可得对数似然函数［式(14)］。

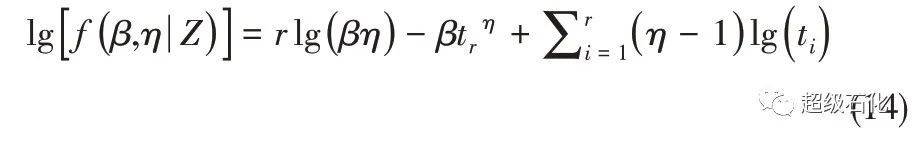
3 案例分析

通过分析蜡油加氢装置系统中的紧急泄压阀来验证该算法的有效性与准确性。安装在蜡油加氢装置冷高压分离器装置（图3）上的紧急泄压阀，其泄放保护对象涉及加氢反应器、热高压分离器和冷高压分离器，在动作时可快速将整个高压系统的压力降低，及时避免危险的发生，所以保证其泄放能力，评估其可靠性至关重要。

当加氢反应器内温度或压力超标时，控制回路可自动调节冷氢量或停止加氢反应。蜡油加氢装置系统同时设有0.7MPa 自动泄压措施和2.1MPa/min紧急泄压系统，用以调节装置压力。当温升小于10℃/min，利用0.7MPa/min自动泄压措施进行降压，若自动泄压措施控制不了温升（温升大于10℃/min），或者反应温度达到453℃，立即启动2.1MPa/min 紧急泄压系统进行降压，保证装置的安全运行。

紧急泄压阀装置的结构如图4 所示。XSOV*A与XSOV*B是2个由IS 1014提供信号控制的两位三通电磁阀。当加氢反应器内温度或压力超标时，由IS 1014 提供信号，将XSOV*A 打开，此时冷高压气经过XSOV*A及其泄放管线泄放，而XSOV*B及其泄放管线起到备用作用，当XSOV*A及其泄放管线无法正常泄放时，冷高压气可以通过XSOV*B及其泄放管线泄放。

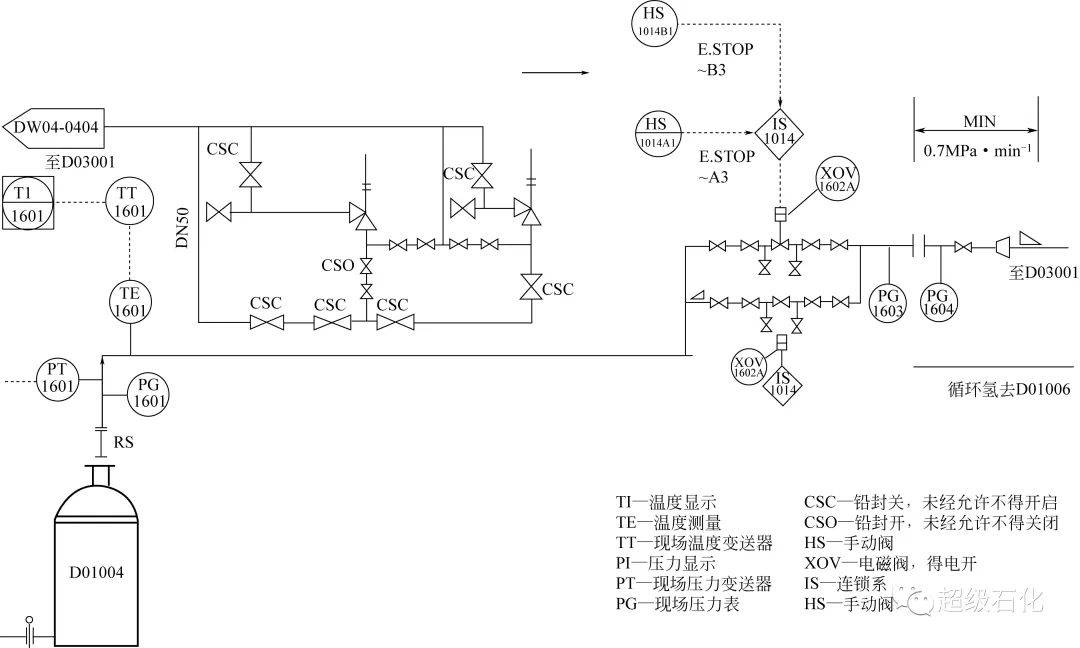
图3 某蜡油加氢装置系统部分工艺流程

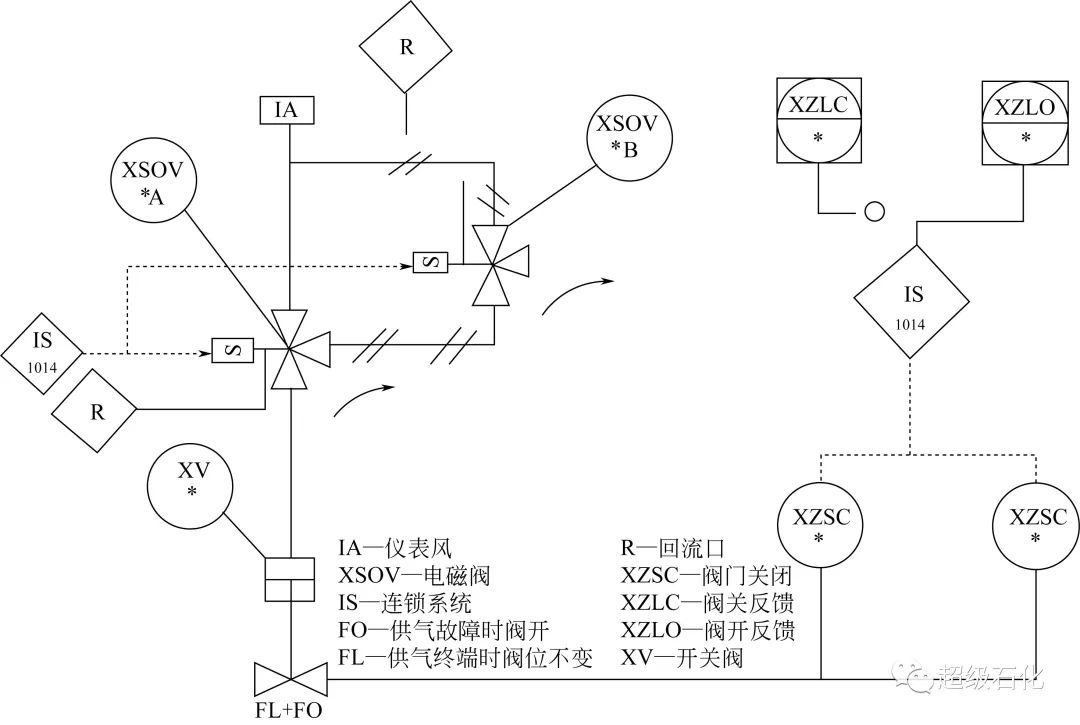
图4 紧急泄压阀

紧急泄压阀是蜡油加氢装置平稳运行的关键保障，对于紧急泄压阀的泄放能力不足，可以通过周期性监测统计蜡油加氢装置系统中的故障时间所处区间情况。设置监测周期为两年，现场定期监测的周期为1460h，则在监测周期内共有12个定期观测区间，为便于比较，不失一般性，采用Monte Carlo方法模拟获得紧急泄压阀运行初期的故障数据，在设备可靠性增长过程中0＜η＜1，故障间隔时间随机增加，设置强度参数、形状参数的初值分别为：β=0.2，η=0.6，见表1。

通过监测策略确定出每个观测区间里的故障数，见表2。

根据紧急泄压阀的模拟故障数据，设置形状参数的迭代初值η(0)=0.4，利用逆变换区间截尾数据填充算法获得区间缺失数据，通过MCEM 算法进行参数估计迭代，设置迭代终止条件ε=0.001，最终评估结果为β̂= 0.259477,η̂= 0.558142。共进行7次迭代计算即满足迭代终止条件，参数估计及评估结果见表3。

表1 60个紧急泄压阀模拟故障数据

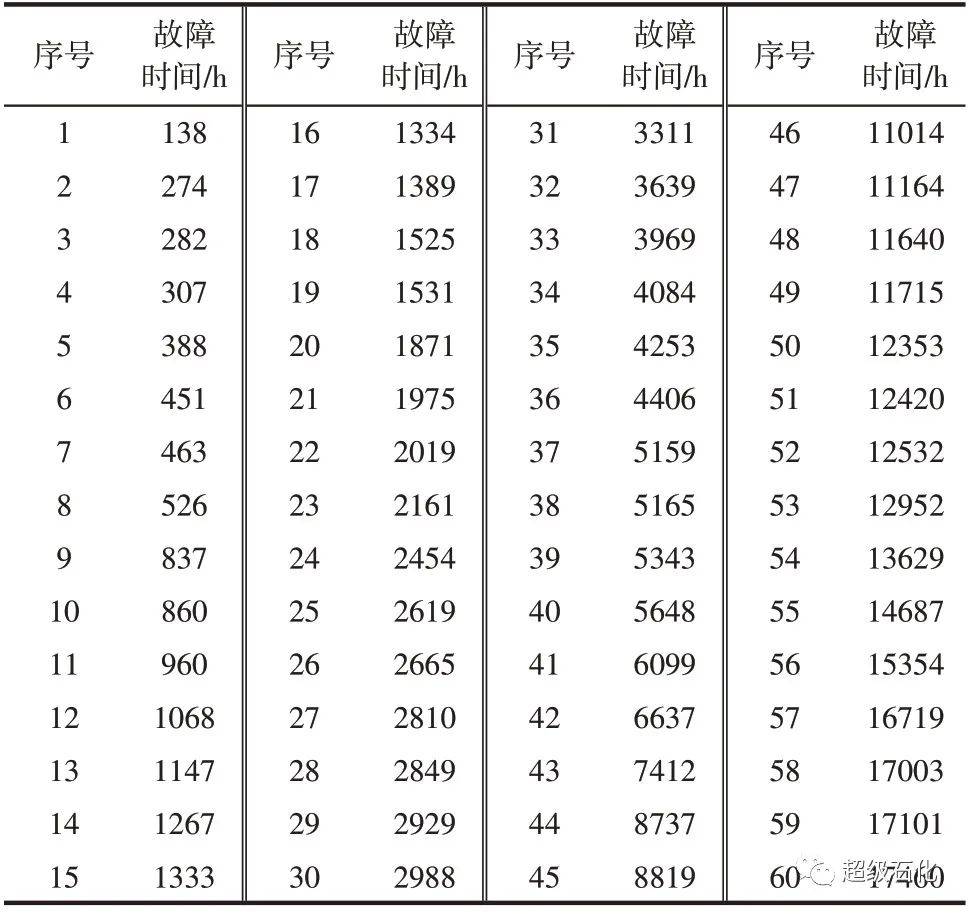
表2 区间缺失数据个数

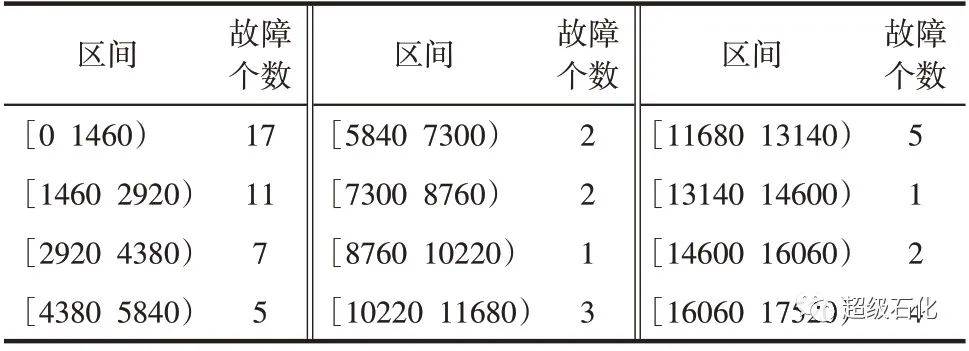
表3 模型参数估计及评估结果

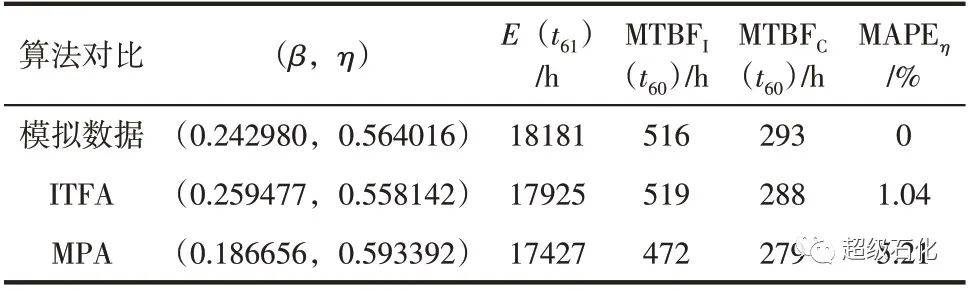
注：MAPEη表示η的平均绝对百分误差；MTBFI(t60)、MTBFC(t60)分别表示设备第60次故障的瞬时平均故障间隔时间和累积平均故障间隔时间。

根据表3可以发现，中值填充法所得的可靠性指标误差较大。以E(t61)为例，在形状参数η不变的前提下对比第61 次设备预计故障时间，文中算法的预测误差为256h，相对误差为1.4%，相对误差较小，说明预测结果可以接受。同时，该算法所得结果较中值填充法提前了498h，设备维护人员可通过预测结果对紧急泄压阀进行合理的检维修工作安排。进一步，选取不同迭代初值验证该算法对迭代初值的敏感性情况，结果见表4。

表4 不同迭代初值及评估结果

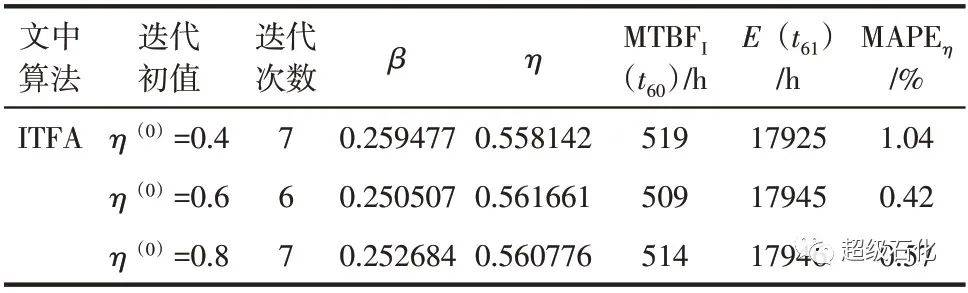
从以上结果可以看出，该算法对迭代初值的敏感性不高，在一定次数下均能得到较为精确的结果，具有稳定性好、可在一定迭代次数下收敛的优点。值得注意的是，由于该算法通过样本均值实现对总体均值的近似替代，其参数收敛速度不如EM算法参数收敛速度快。同时利用该算法得到的可靠性指标与模拟数据偏差很小，形状参数估计值的偏差较中值填充法缩小了4%以上，有效降低了数据不完整对可靠性评估的影响，使设备维护人员获得更好的紧急泄压阀可靠性评估结果。图5展示了两种填充算法的数据填充对比情况，可以看出文中算法的填充数据与模拟“真值”数据的拟合度较高，说明了该算法具有较高的准确性，很好地解决了实际生产中区间截尾的数据缺失问题。

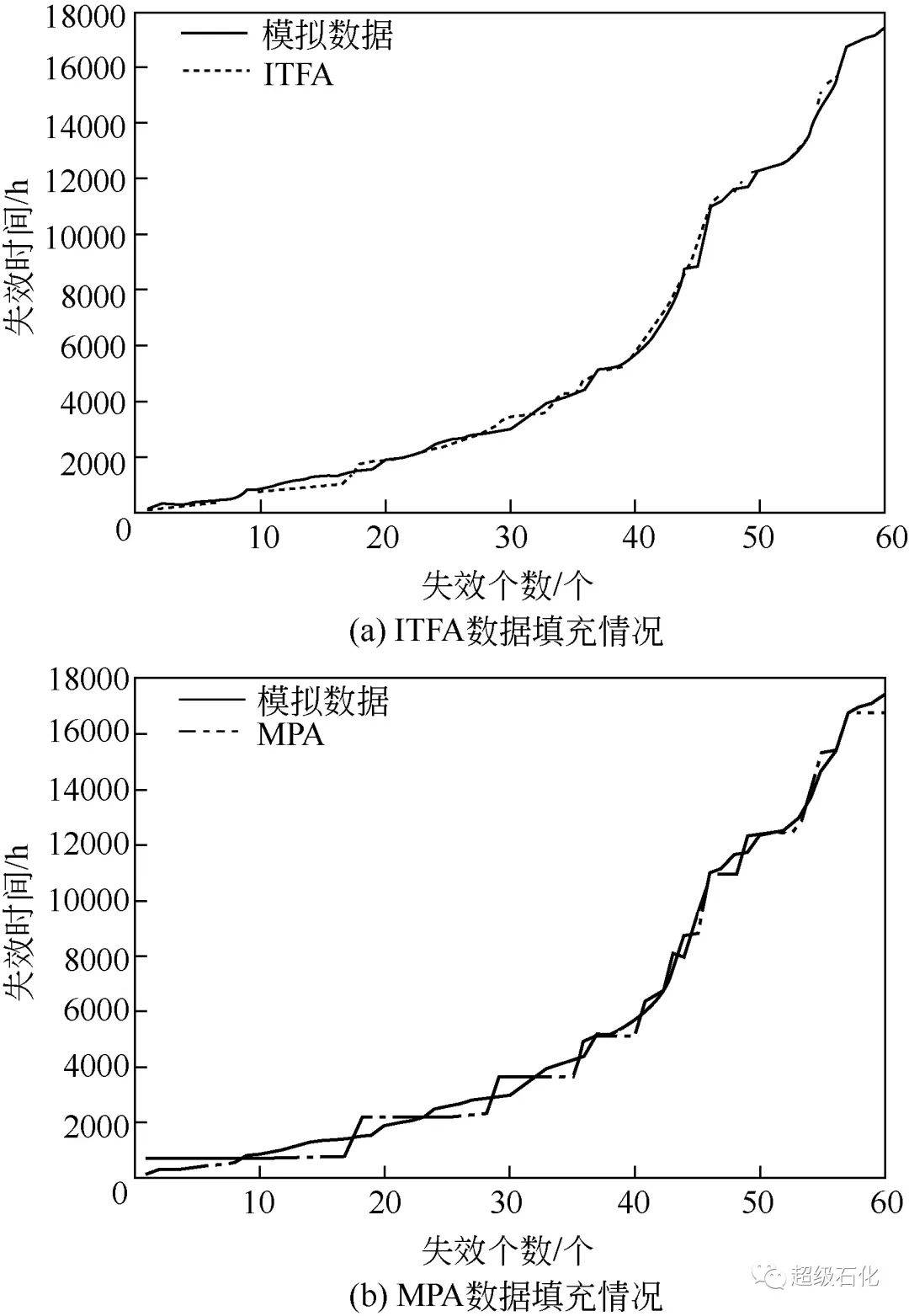
图5 数据填充算法对比

图6进一步展示了两种填充算法下的可靠性指标对比情况，可以看出随着观测时间的延长，平均故障间隔时间也在增大，这对应了在运行初期紧急泄压阀处于可靠性增长的趋势。根据图6，在紧急泄压阀运行至17384h时，累积平均故障间隔时间仅有288h，但瞬时平均故障间隔时间为519h，表明在短时间内设备发生故障的概率较小，因此不建议在当前时刻采取相应措施进行检修，建议考虑在17903h时刻再进行维修，对比文中算法得到的第61次设备失效的预计时间E(t61)=17925h，预测的误差为22h，相对误差仅为0.12%，既避免了造成维修成本的浪费，又兼顾了生产系统的平稳运行。此外从图6可以看出，利用中值填充法得到的可靠性指标比逆变换填充算法得到的结果偏小，以第60次故障为例，瞬时平均故障间隔时间的相对偏差为7.9%，累积故障间隔时间的相对偏差为3.0%，表明中值填充法得到的可靠性指标相对保守，这会使得设备维护人员对运行初期紧急泄压阀的可靠性做出不合理的评估，极易破坏设备的机械完整性和可用性。

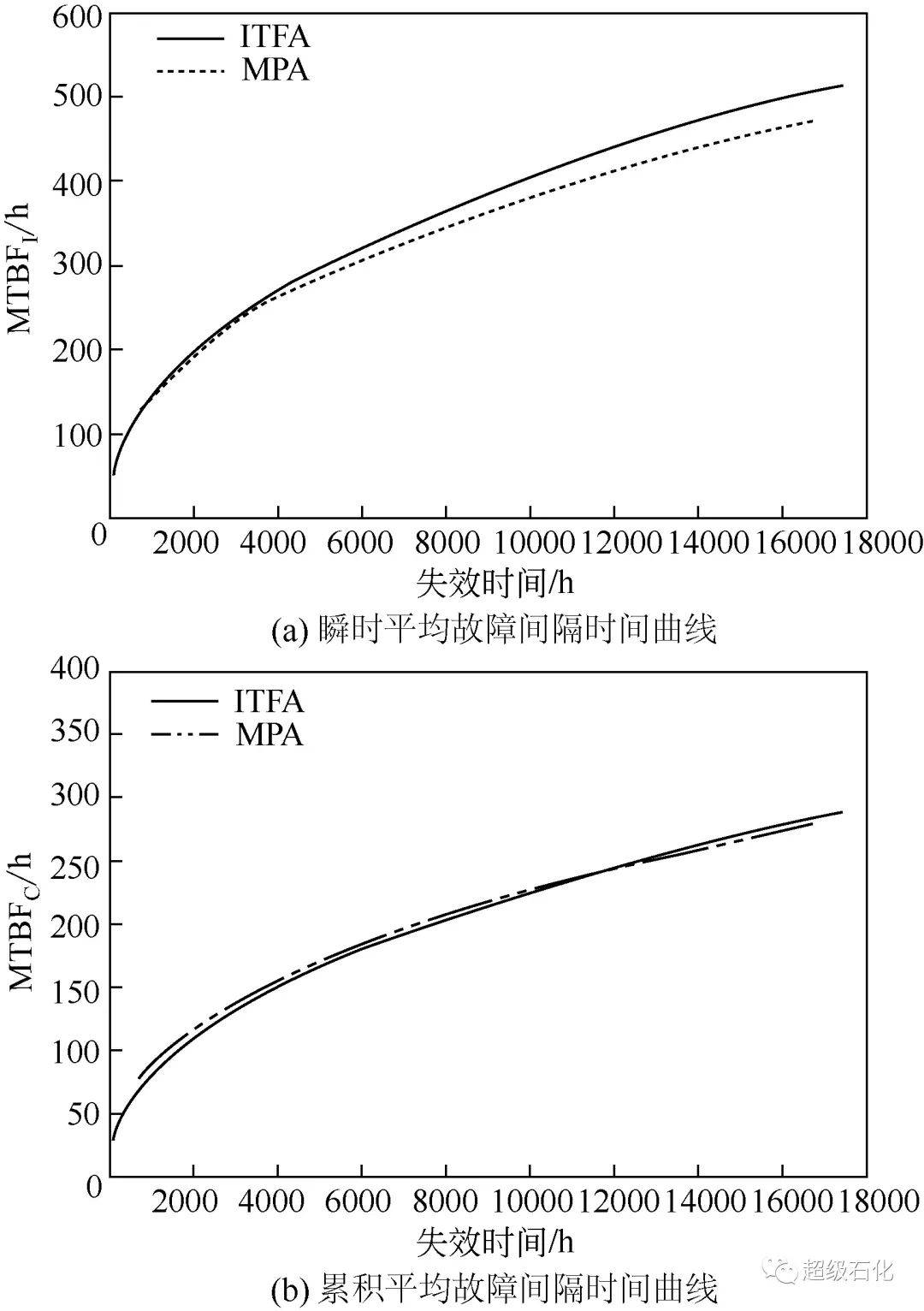
图6 可靠性指标曲线

4 结论

（1）在可修系统基于最小维修的假设下，文中算法能够融合已有的观测数据，简便地实现缺失数据的填充过程，有效降低了数据缺失造成的统计偏差，同时也便于在工程实践中使用。

（2）对比中值填充法，利用文中算法得到的可靠性评估指标更为精确，形状参数估计值的误差缩小了4%以上，并给出了设备下次故障时间的预估值，这有助于设备维护人员准确掌握安全关键设备的可靠性状况，保证设备处于较高的机械完整性和可用性，并为企业的设备维修策略提供一定的理论依据。